1. 트리자료형이란 ?
- 계층적 자료구조.
- Node들로 구성되며, Edge(간선)로 연결되어 있다.
- 가장 상위에 있는 Node를 루트노드 라고 부르며, 각 노드는 0개 이상의 자식 노트를 가질 수 있다.
- 트리에서 노드가 자식 노드를 가지지 않는 경우 그 노드를 리프(leaf)노드라고 부른다.
2. 트리 순회
- 트리의 노드를 시스테마틱한(체계적이고 조직적인) 방식으로 방문하는 과정.
- 트리순회의 목표는 트리의 모든 노드를 효과적으로 방문하는 것이다.
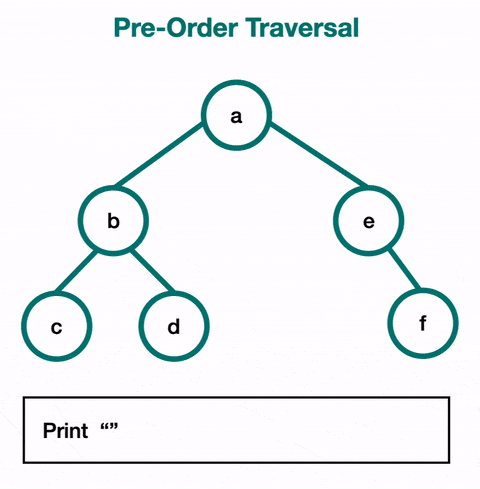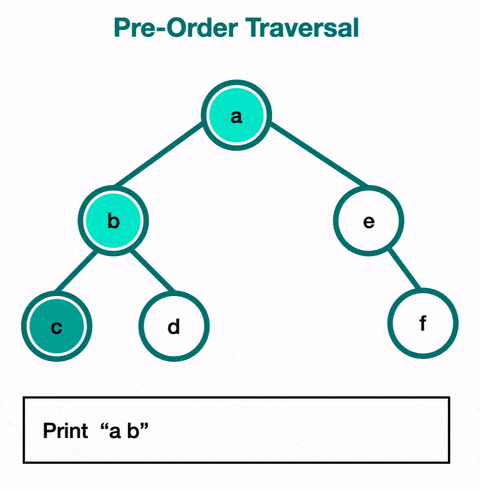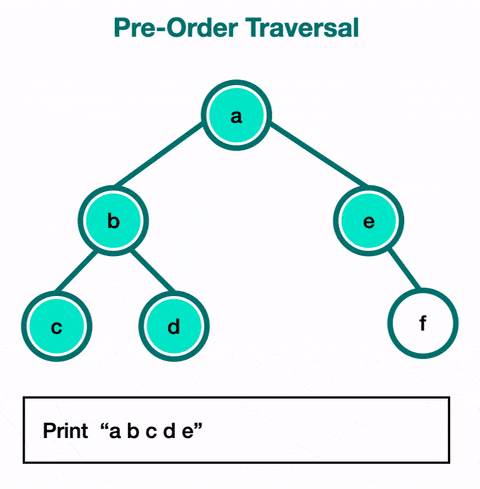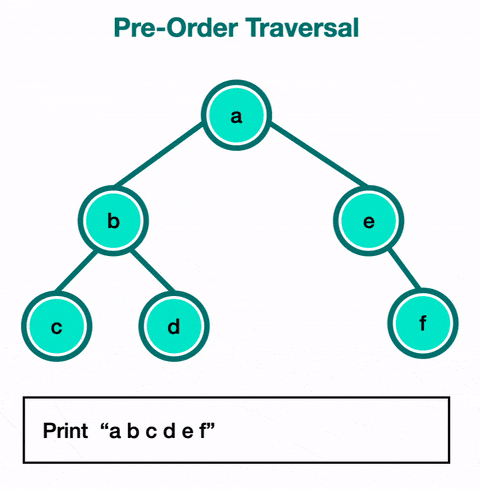
1) 전위 순회 (Pre-order Traversal) :
전위 순회에서는 루트 노드를 먼저 방문한 후, 왼쪽 서브트리를 순회하고, 그 다음 오른쪽 서브트리를 순회한다.
루트 -> 왼쪽 -> 오른쪽
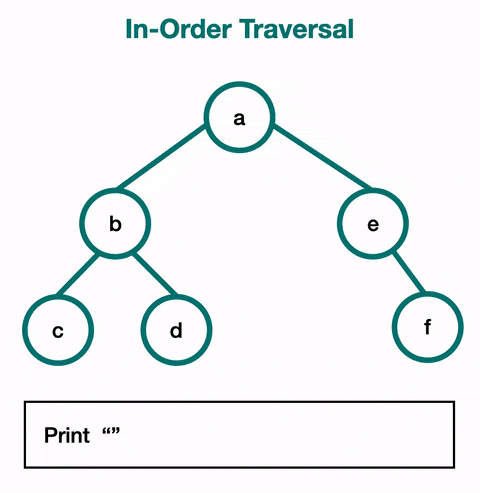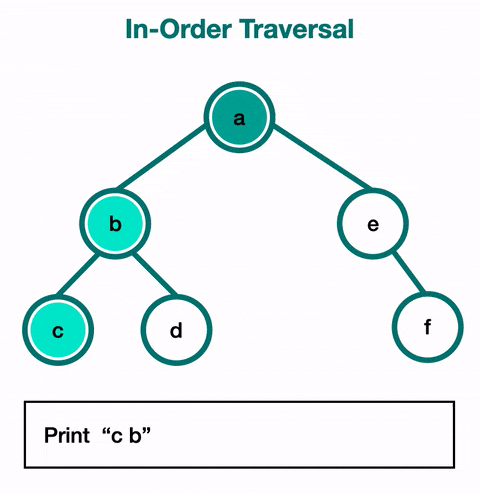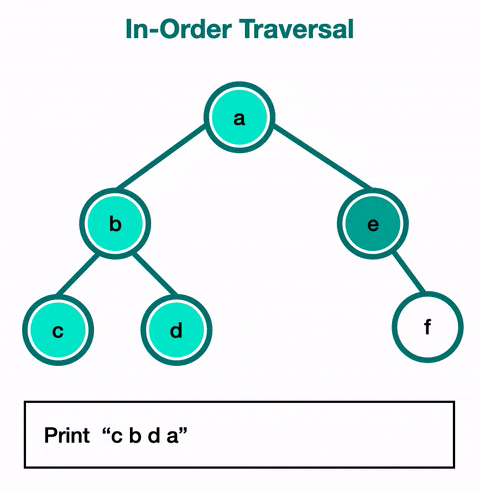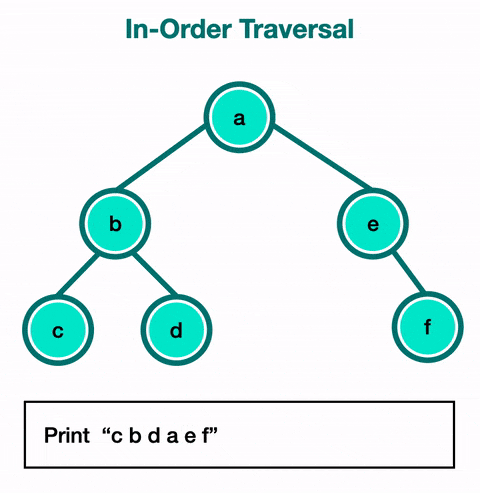
2) 중위 순회 (In-order Traversal) :
중위 순회에서는 왼쪽 서브트리를 먼저 순회하고, 루트 노드를 방문한 후, 오른쪽 서브트리를 순회한다.
이진탐색트리에서 노드를 오름차순으로 방문할 때 사용한다.
왼쪽 -> 루트 -> 오른쪽
3) 후위 순회 (Post-order Traversal) :
왼쪽 서브트리를 먼저 순회하고, 오른쪽 서브트리를 순회한 후, 루트노드를 방문한다.
왼쪽 -> 오른쪽 -> 루트

3. 특징
- 트리순회는 주로 트리에 저장된 데이터를 처리하거나 분석하는 데 사용된다.
- 각 순회 방법은 특정 작업에 더 적합할 수 있으며, 적절한 순회 방법을 선택하는 것이 중요하다.
- 트리순회는 재귀, 또는 반복을 통해 구현할 수 있다.
- 이진 탐색 트리에서 중위 순회를 사용하면 데이터 정렬/탐색에 유용하다.
- 디렉터리 구조와 같은 계층적 구조를 표현하는데 사용되는 트리에서 전위 순회나 후위 순회가 적합할 수 있다.
- 레벨순회같은 것도 있다.
- 최종적으로, 트리 자료형은 계층적 데이터 구조를 효과적으로 저장하고 조작할 수 있는 방법을 제공하며, 트리 순회 알고리즘은 트리에 저장된 데이터에 접근하고 처리하는 데 사용된다.
4. 구현
1) 이진트리의 간단한 구현(JS)

참고 :
이진 탐색 트리(Binary Search Tree, BST): 이진 트리의 일종으로, 모든 노드에 대해 왼쪽 서브트리의 모든 노드 값이 현재 노드 값보다 작고, 오른쪽 서브트리의 모든 노드 값이 현재 노드 값보다 큰 특성을 가지고 있습니다. 이 특성으로 인해 이진 탐색 트리에서는 효율적인 검색, 삽입, 삭제 연산이 가능합니다.
완전 이진 트리(Complete Binary Tree): 모든 레벨이 꽉 차 있고, 마지막 레벨의 노드들이 왼쪽부터 오른쪽으로 채워져 있는 이진 트리를 의미합니다. 완전 이진 트리는 배열을 사용하여 메모리를 효율적으로 사용할 수 있습니다.
균형 이진 트리(Balanced Binary Tree): 균형 이진 트리는 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 최대 1인 이진 트리입니다. 균형 이진 트리는 트리의 높이가 작게 유지되어 연산의 효율성이 높아집니다. AVL 트리와 레드-블랙 트리는 대표적인 균형 이진 트리입니다.
2) 전위순회 (Pre-order traversal) 구현
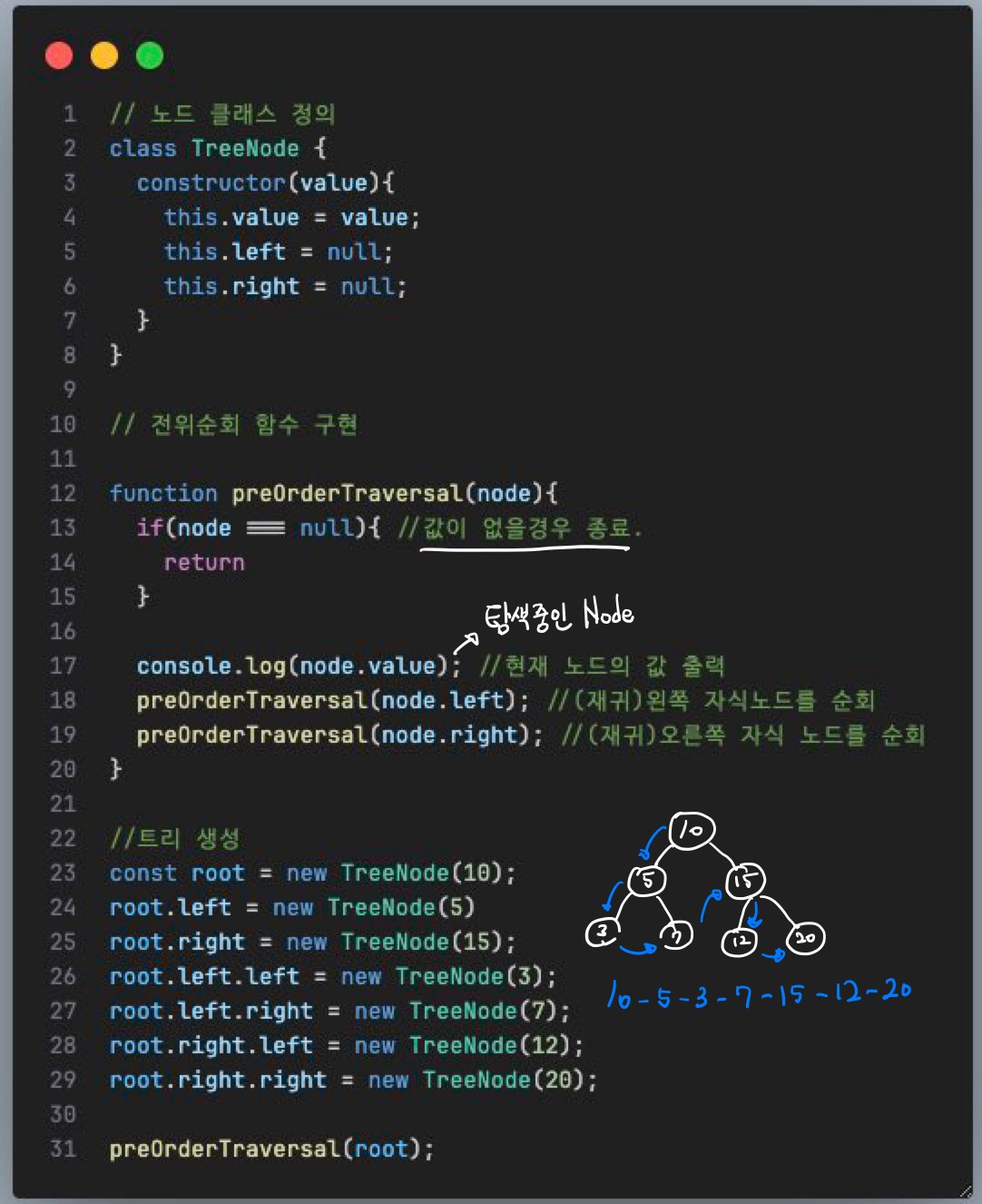
3) 중위 순회 (In-order traversal 구현)
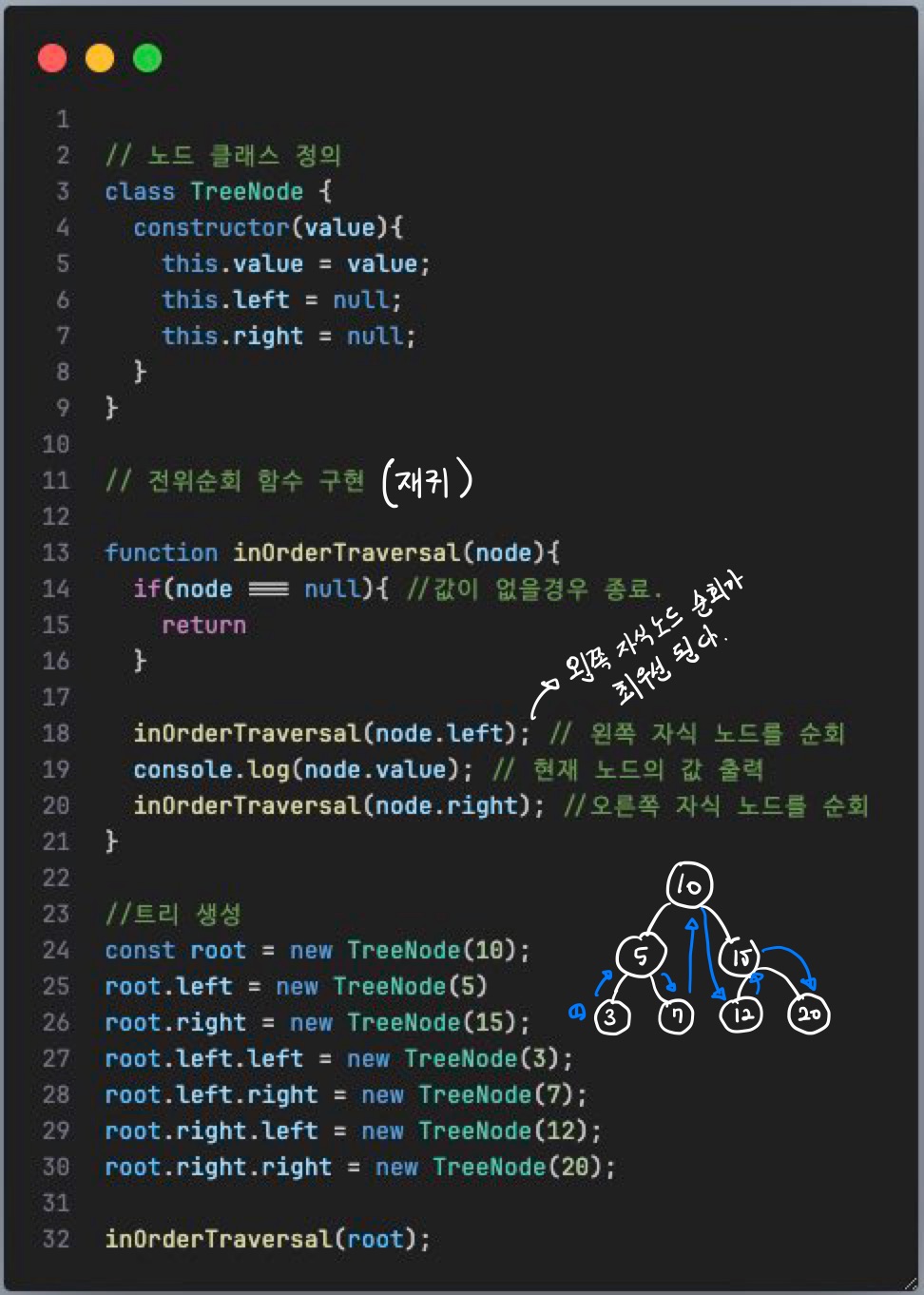
4) 후위 순회 (Post-order traversal 구현)
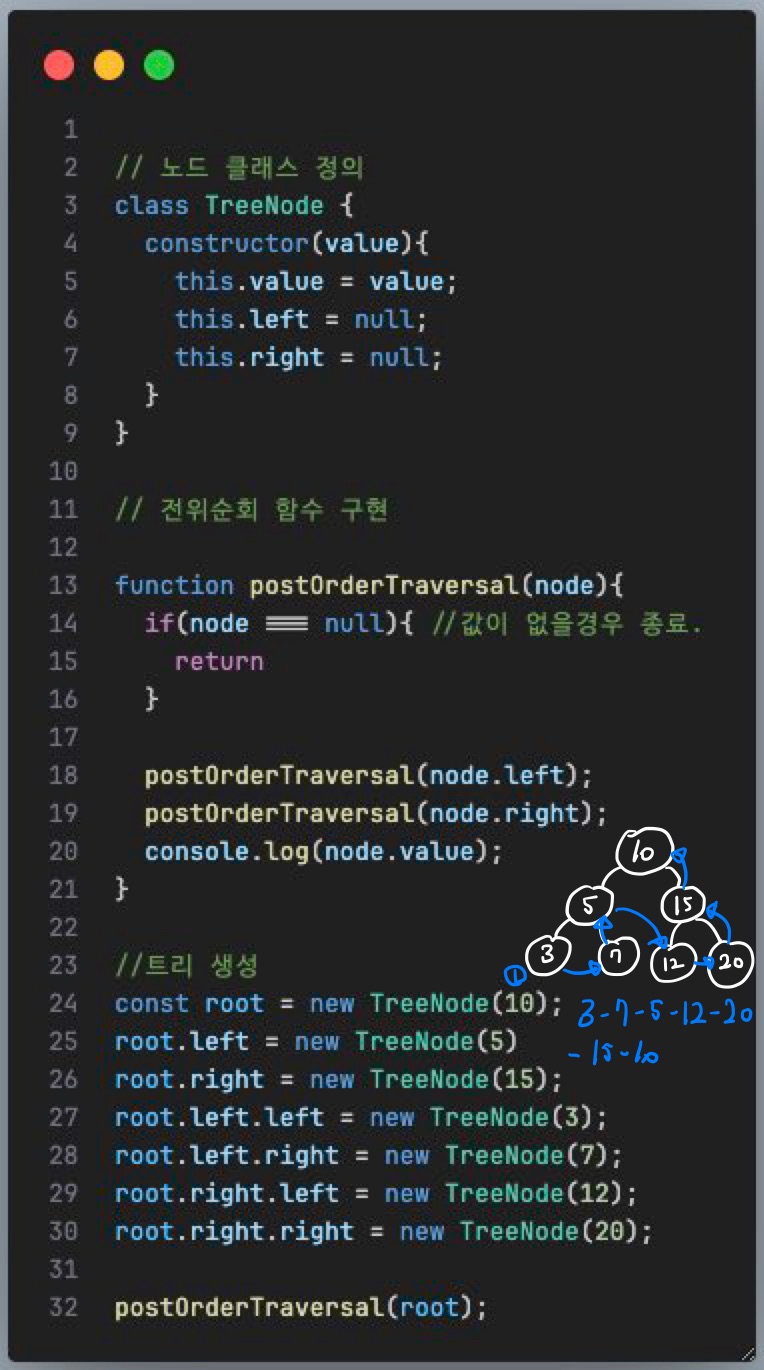
아고 쉽다 !
'ComputerScience > 알고리즘, 프로그래머스' 카테고리의 다른 글
| [Algorithm] 완전탐색 (JS) - 2 : 백트래킹(Back Tracking) (0) | 2023.04.04 |
|---|---|
| [Algorithm] 완전탐색 (JS) - 1 : 브루트 포스(Brute Force) (0) | 2023.04.04 |
| [Algorithm] Graph-Theory - 3 : DFS와 BFS 한방에 이해하기. (0) | 2023.04.03 |
| [Algorithm] Graph-Theory - 2 : JS로 구현과 시각화 (0) | 2023.03.31 |
| [Algorithm] Graph-Theory (0) | 2023.03.31 |




댓글